 PDF(13428 KB)
PDF(13428 KB)


 PDF(13428 KB)
PDF(13428 KB)
 PDF(13428 KB)
PDF(13428 KB)
Al-4%Cu凝固过程枝晶生长的数值模拟
 ({{custom_author.role_cn}}), {{javascript:window.custom_author_cn_index++;}}
({{custom_author.role_cn}}), {{javascript:window.custom_author_cn_index++;}}Numerical Simulation on Dendrite Growth During Solidification of Al-4%Cu Alloy
 ({{custom_author.role_en}}), {{javascript:window.custom_author_en_index++;}}
({{custom_author.role_en}}), {{javascript:window.custom_author_en_index++;}}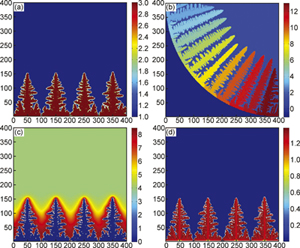
| {{custom_ref.label}} |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
/
| 〈 |
|
〉 |